Hand Evaluation
last update: 20 February 2022
Introduction
The core topic treated on this webpage is 'hand evaluation' rules, which includes point counting, distributional points, controls, losing trick count, and total number of tricks. The last and largest section on this webpage concerns the understanding and evaluation of 'shape'. This topic is vital when looking to go beyond just adding distributional points to high-card points, and hoping for the best.
Good bidding is based upon knowing and using a well-structured system. But the application of a good bidding system needs good judgement, and the first step to good judgement is intelligent hand evaluation.
Let's have an example of what hand evaluation means in practice. Have a look at these two hands…
West ♠A-K-Q ♥A-6-5 ♦Q-4-3 ♣7-5-3-2
East ♠J-7-6 ♥K-Q-J ♦J-7-5-2 ♣J-10-4
West would open 1NT (15-17 HCP) and East would invite 2NT (8-9 HCP), West passes. Making 7 tricks might be a problem. Now consider these two hands …
West ♠A-K-Q ♥A-J-6-5 ♦J-4 ♣9-7-3-2
East ♠J-7-6-5 ♥K-Q-2 ♦Q-7-5 ♣J-10-4
Same honour cards, more or less the same distribution, and the resulting contract would be the same, 2NT. Now 2NT would be easy, against any defence. What's the difference? Small shift is distribution with West (4-3-3-3 to a 4-4-3-2), and a ♣9 instead of a ♣5.
Now consider these hands…
West ♠K-Q-7-6-4 ♥K-Q-3 ♦6-5-4 ♣K-8
East 1 ♠A-J-10-8-2 ♥4 ♦A-10-9 ♣A-7-6-3
East 2 ♠A-J-10-8-2 ♥A-10-9 ♦3 ♣A-7-6-3
With East 1 Opponents need to duck the first attack in ♥'s, otherwise East-West can use ♥K-Q to discard ♦10-9. So a slam is unlikely, and East-West make 5♠'s. Just swapping the ♥'s and ♦'s in East hand, and 6♠'s is easy.
Hand evaluation is all about identifying the above differences and translating them into winning contracts. This means determining the hand's 'value' (usually a number), and communicating (bidding) this number to their Partner. The trick is to pass the maximum information (within the rules), but keep the hand evaluation simple yet meaningful.
Hans evaluation should become a second nature for a bridge player, but it becomes vital in knowing when to compete with Opponents for a contract, and just how far they can go, and in knowing when to bid a slam and when to stop.
So hand evaluation is about how Partners assess their hands and describe them to each other so that they can reach the optimum contract (i.e. best chance of scoring the most points with a reasonable risk).
The problem appears to be that there is no one single way to look at hand evaluation, so it's up to the players to work towards what they consider the best options for their skill level, etc. I've tried to put down as much as I can find and remember, and I hope it useful and not too confusing.
The value of a hand depends upon the quality of its high-card strength (honour point count or high-card points) and the length of the suits (distribution), and to a lesser extent the location of the honour cards. What each player needs (and each partnership must agree on) is a way to evaluate the combined high-card points and distributional strength of a variety of different types of bridge hands.
Another important feature is the way hand evaluation must change during the bidding. Hand evaluation is about determining the playing strength of the hand in relation to the other three hands. There are three situations which will always influence hand evaluation during the bidding. Firstly, the advantage/disadvantage of short suits. Secondly, the fit with partner and/or the opponents finding a fit. Thirdly, the favourable or unfavourable position of high cards. The goal of the bidding is to find a 8+ card fit in a major suit, and all the players at the table will evaluation their hands with that in mind. Without an 8-card fit, the players will move their focus to the next best thing, a contract in No Trumps. This will require a re-evaluation of the strength of the hand. If that fails then the remaining option is a contract in a minor suit. That again will require a new re-evaluation. Finding support from partner, finding a strong hand with partner, a double by opponents or partner, the interventions of the opponents, even a Pass by anyone at the table, all will require each player to re-evaluate their hand 'on-the-fly'.
As an example, this hand ♠10-5-3-2 ♥Q-J-10-7 ♦8 ♣9-8-5-3, has 3 high-card points (HCP) plus 2 distribution points for the singleton, so 5 points DH (DH means distribution+HCP). A good initial position is that this is a 'Pass' hand, however it could be interesting in defence (4-4 majors, a singleton, and a possible bad HCP split against the opponents). But Partner opens 1♥, so what to do now? 'Pass' or re-evaluate. Many players will not 'see' beyond the 3 HCP or the 5 DH. However, this hand has 3 HCP's all usefully placed in partners suit, 3 more points for the singleton (an extra point for the singleton with a fit with partner), plus an extra point for the 4-card support, and on top of all that a couple of 10's and a 9-8 sequence could be worth an extra point. So now the hand has a worthwhile 7-8 DH, and Partner should support Opener with a bid of 2♥. This logic would be just as valid if Opener bid 1♠.
Below we look at ways to evaluate both the high-card strength of a hand and its distributional strength. We will also look rapidly at different ways to evaluate a hand by its controls or by the so-called 'losing trick count'. The Wikipedia article on hand evaluation is a good companion text. And finally we will focus on a long section about determining and exploiting a hand's 'shape'.
On these webpages I use the abbreviation DH to mean 'Distribution+HCP'.
Milton Work Point Count
Bridge players need some simple and practical way to start evaluating a bridge hand. What to take into consideration - high cards, suit distribution, quality of suits, controlling cards, fit with partner, general 'shape', …? The most basic and certainly the most popular evaluation method (initially conceived for a 'balanced' hand) is to assign numerical values to the top four honour cards.
Point Count: Ace = 4 HCP King = 3 HCP Queen = 2 HCP Jack = 1 HCP
There are 40 total high card points (honour point count) in the deck, and the addition of the points in a particular hand is known as the high-card point (HCP) count. An 'average' hand would be expected to hold 10 HCP in the form of 1 Ace, 1 King, 1 Queen, and 1 Jack.
Simply put, you need a better than average hand (say 12 HCP) to open the bidding.
Based upon a large sample of real world bridge hands just using HCP is insufficiently precise. It does not take hand shape into account, and there are several ways to refine the way players should assess (or re-assess) the exact distribution of cards in any specific hand. Statistical analysis of hands show that HCP undervalues Aces and 10’s, other analyses prefer to consider Queens and Jacks as overvalued. In the real world Queens and Jacks often fall under Aces and Kings rather than win tricks, and in defence a Jack hardly ever wins a trick. There are several ways to 'adjust' HCP's, the ones I like are (i) add 1 HCP when holding all 4 Aces, (ii) deduct 1 HCP if a hand has no Aces, (ii) add ½ HCP for each 10 in a hand.
Many texts mention Charles Goren as the creator of the 4-3-2-1 point-count system. As Wikipedia points out Goren developed the ideas of Milton Work and again as Wikipedia rightly notes the point-count system was based upon a suggestion made in 1915 by Bryant McCampbell as a way to evaluate balanced hands. Initially Work opposed the point-count system, but finally he was responsible for promoting the system from 1927. Goren was an employee of Work and it was he that applied the point-count to value all types of hands.
The reality is that the Work point-count is just one of many high-card point counting systems. Without introducing other point-count systems it is still possible to see where experts feel the present-day system fails. There appears to be two weaknesses that should be recognised. Firstly, Aces are undervalued, with some experts introducing a bigger point gap between Kings and Aces. Secondly 10's are ignored, but many experts attribute a ½ or 1 point to a 10. Some but not all experts appear to down grade the Jack, and some give a ½ point to both the Jack and 10.
According to the experts the 'best bet' might be to give 5 points to an Ace, 3.5 points to a King, 2.3 to a Queen, 0.9 to a Jack, and 0.3 to a 10, but this would require a complete revision of the point-count system for partial and game contracts, etc.
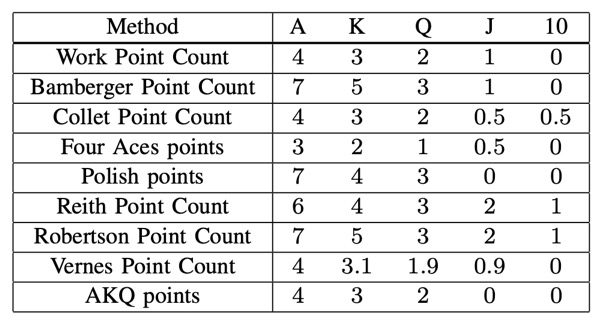
Above is a table low the different High Cart Point counting systems proposed by different authors. They don't all agree, but the key message is that experts think that Aces and 10's are more valuable than the point-count suggests.
However computer simulations of 1,000's of hands tells us something even more interesting. One of the key messages is that if you are playing a particular suit contract the Ace, King, etc. in that suit are more valuable than the same cards in another suit. If we look at the simulations the Ace of trumps is still worth 4 points, but the King (3.3 points), Queen (2.7 points), Jack (2.2 points) and 10 (1.8 points) are all worth more than a simple high-card point-count would suggest. So the Ace of trumps is still worth 4 points, but the other Aces are worth only about 2.3 points. Other honours in the side suits are worth less than the same face-card in trumps or in the preferred side suit. We all know that the Jack in a short side suit is not likely to be useful, and in fact the simulation tells us that Queens, Jacks and 10's in short side suits are (on average) not worth much (unless Declarer need to exploit that particular side suit).
Clearly any specific hand might well need a good side suit and the Queen, Jack and 10 in that suit will be worth more, but on average they are worth much less. And Aces in side suits permits the declarer to 'control' the way the hand plays out, and can be far more valuable than having a couple of unproductive Queen-Jacks in side suits.
But what is really impressive is the value of small trump cards. The 10 is worth 1.8 points, the 9 is worth 1.6 points, the 6-7-and 8 are worth each about 1.4 points, and even the 5, 4, 3 and 2 of trumps are worth about 1.3 points each. This sounds reasonable because small trump cards will usually be correlated with longer trump suit holdings. Small cards in other suits are worth nothing, and what is surprising is that a simple 2 of trumps can be worth almost as much as a King (1.4 points) when 'exposed' in a difficult to exploit side suit.
In fact during the description of many bidding systems there are hints that 3-card support for Openers major can mean a lot more than just a 'fit'. Holding more trumps is worth more that holding honour cards in a 'useless' side suit. Holding a 5-4-3 in trumps is collectively worth about 4 points, and can be worth the same as an Ace and a badly placed King in side suits. We now understand better when experts say a partner holding x-x-x in trumps is nice but a partner holding K-x-x support in trumps is better (it can be worth 6 points).
We also now understand why an extra trump is worth its weight in gold because 9-x-x-x is worth as much as Q-x-x in trumps (and that means that those 2 high-card points can often be better used elsewhere). We can start to see why experts are willing to play game with a 10-card major and a 20-20 break in points. If a partnership has 10-cards headed by just A-K then having Q-J or x-x in trumps is the same, and the 3 HCP are probably more useful elsewhere.
The real difficulty in a trump contract is how to evaluate the hand during the bidding. The value of the honour cards will be different before and after the trump contract is decided. A 2 of ♠ could be quite valuable as the 9th card if ♠ are trumps, but worth less than nothing otherwise (holding a 2 in a side suit has a negative impact on the overall strength of the hand when playing in a different suit). Here we see the logic in re-evaluating the hand once a trump suit has been decided. But does that re-evaluation go far enough? Again we can now see the logic in a bidding sequence such as 1♠ - 2♠ - 3♦ - 4♠ which allows the partnership to upgrade the point-count for the second suit (♦) and downgrade 'wasted' honours such a Queen or Jack in a useless side suit.
If we turn to the computer simulation of No Trump contracts, we can see that having a nice 5-card suit can be worth more than having exposed high-point cards. In fact Aces are worth about 4 points and Jacks are worth about 1 point, but Kings and Queens are slightly over valued. We all know that a K-Q is worth just a bit more than an Ace, i.e. they are worth together only about 4.4 points and not 5 points (and as a doubleton they are only worth the same as an Ace). A 10-9 pair is worth about the same as a Jack, and smaller cards provide distributional support which we all know is useful in No Trumps despite the 'tradition' to only count high-card points for this type of contract.
Rule of 20
Above we mention counting "points", and the need for at least 12(13) to "open" the bidding. But another way to help decide if you should open is the Rule of 20, which decide if "marginal" hands are worth an opening. The Rules is simple "If the number of points plus the number of cards in the two longest suits is 20 or more, open".
If the number is 19 or less, depending on the long suits, you may choose to open with a weak 2, but should not open at the 1st level. As a warning the rule does not focus on Aces or "quick tricks". Thee are useful little rules that help, such as a totally flat hand (4-3-3-3) and a minimum 15 HCP, without an Ace is too weak for an opening 1NT. Similarly, with the Rule of 20, you should still have at least an Ace, or better still 1.5-2 "quick tricks". A quick trick is an Ace, AK suited or two Aces are two quick tricks. And they work best if they are concentrated in long suits. So, a more detailed and better functioning rule would be:
Precise rule of 20 (or 22)
Let’s look at some marginal hands and apply this methodology to determine if we should open the bidding…
♠A-K-x-x-x ♥Q-J-x-x-x ♦x-x ♣x
10 HCP + 10 cards in two longest suits = 20 (+ two quick tricks = 22), so open 1♠
If the number of points + the number of cards in the two longest = 20 + working quick tricks is >21, open the bidding. Note it is >20, and not = 21.
♠A-K-x-x ♥Q-J-x-x-x ♦x-x ♣x-x
10 HCP + 9 cards in the longest suits = 19 (+ two quick tricks = 21), Rule of 20 failed
♠K-x-x-x-x ♥x ♦K-J-x-x-x ♣Q-J
10 HCP + 10 cards in the longest suits = 20 (+ 1 quick trick = 21 and not >21). A very marginal hand.
Some of the >21 hands ‘look’ too weak to open at the first level, but both experience and statistics suggest that following the rule of 20(22) succeeds more often than not. Of course, you are not obliged to open such hands, but the Rule of 20 tells you if a 1st level opening is a reasonable option.
This is not a "law", it's just a rule to be used with caution. For example, the quick tricks should be in your important suits. And intermediate cards can change your impression of the hand, in both ways.
Distributional Points
Players should supplement the HCP with distributional points, either suit length or suit shortness. When playing in a suit I prefer to count ruffing potential, e.g. suit shortness. Initially I add 3 points for a void, 2 for a singleton, and 1 for a doubleton. However once a 'fit' (usually meaning 8 cards in a suit) has been found I will tend to count 5 points for a void, 3 for a singleton, but keep just 1 point for a doubleton. This type of distributional point count works well for 'three-suit' hands, but some players prefer to re-evaluate the distributional strength of their hand only when they are going to be dummy and only when they have the necessary trump support (avoiding both partners counting extra distributional points for the same suit).
An analysis of real world bridge hands shows that using HCP and distributional points correlates better with tricks won. It's not perfect, but it is better.
With 'two-suit' and 'one-suit' hands it is often better just to count 'playing tricks' rather than distributional points (or 'Losing Tricks' as we will see below). The problem here is to have a good partnership understanding on the definition of playing tricks and/or on using losing trick counts. Some experts define playing tricks as a number of expected tricks with no help from partner (e.g. a void in the suit). Others use it for strong hands and assume a reasonable distribution of cards and HCP around the table, including in partners hand. Most experts agree that it applies to hands with 16+ HCP.
I've seen some experts consider adding 'playing tricks' and 'losing tricks' together to make 13. The more you have one, the less of the other.
Yet other experts talk about 'clearcut tricks' when opposite a void in Partners hand, and others increase the DH value of the partnerships 2nd best suit.
And finally some experts appear to equate 'playing tricks' with 'controls' or 'quick tricks', and add value for every card from the 4th in their long suit.
Some players will add additional distributional points for long suits. e.g. 1 point for any 6-card major suit and 2 points for any 7-card major suit. With these declarations it is sensible to only add the points if the long suit also holds at least two of the top three honours, or three of the top five honours. This is the basis of most pre-emptive bids.
The addition of 3 points for a void, etc., and the negative point adjustment for unprotected honours, and the extra points for long suits, the 4 Aces and for 10's are together called the Pavlicek Point Count. An important point here is that 13 Pavicek (total) point count becomes the threshold for making an opening bid. Pavlicek also added a couple of additions. Firstly he adds a point for any suit in dummy that is Qxxxx or better. Equally he adds 1 point for a 5-card suit if partner raised the suit without knowing it was a 5-card suit. He adds 2 points for every trump card over five if they had not been 'shown' to partner. And finally he adds an additional point for each card over three in a side suit. Adding everything together he sets game firmly at 26 points.
There are many different ways to allocate distributional points, some players add points, some subtract points, and others mix the points up. We have honour trick counting with 2 points for an Ace, 1½ point for A-Q, and 1 point for KQ. There are playing tricks points with an extra point for a 5-card suit with honour cards, 2 extra points for a 6-card suit with honours, etc., and an extra point for the Ace and for the King in trumps, and the same for Q-J in trumps, but just a ½ point for a Q or J-10. The losing trick count counts the tricks to loose in the first 3 cards of each suit (we will look at this option below). The 'asset point system' adds points to the high-card point-count with 2 points for a void, 1 point for a singleton, and 1 point for a 5+ card suit. Another distribution point system added 1 point for the 5th card, 1 point for 6th card, etc. in trumps, and 1 point for the 4th card plus 1 additional point for the 5th card in one side suit. Another system added one point for a biddable 4-card suit, plus 1 point for the 5th card, plus 2 points for the 6th card, plus 3 points for the 7th card, etc. (this system required 28 DH for game).
One distribution point system subtracted 1 point for no Aces, 1 point less for suits with unprotect honour cards, ½ point less for suits holding less than the 3 top honours, and ½ less for no 10's. Another system added ¼ point for each Ace, ½ point for each 10, and ½ point for suits with 2 of the three top honours.
Point Count Adjustment
Following Evaluation of the Hand – Point Count Adjustment.
In the above introduction we mentioned that simply counting points does not take into consideration the following:-
Length of the suits (distribution)
The location of the honour cards
The advantage/disadvantage of short suits
The quality of the fit with partner
The favourable or unfavourable position of high cards
The general undervaluing of Aces and 10’s, and in particular an Ace in a side suit
The overvaluing of Queens, Jacks and 10's in side suits, etc.
Are Aces so important?
West ♠6-3 ♥A-Q-6-4 ♦A-K-Q-J ♣6-3-2
East 1 ♠Q-J-7-4 ♥K-J-9-3-2 ♦7 ♣Q-J-10
East 2 ♠9-8-7-4 ♥K-J-9-3-2 ♦7 ♣A-9-4
Both East's should end in 4♥, but East 1 will lose the first four tricks for -1.
Simply replacing 2 Q's and 2 J's with an Ace, and East 2 will make an over trick.
As mentioned in the introduction an Ace in side suits permits the declarer to 'control' the way the hand plays out, and can be far more valuable than having unproductive Queen-Jacks in side suits.
Are Aces as valuable in NT?
West ♠6-3 ♥6-4 ♦A-K-Q-J-4-3 ♣K-3-2
East 1 ♠A-K-4-2 ♥K-J-3-2 ♦10-2 ♣9-8-6
East 2 ♠A-K-4-2 ♥A-7-3-2 ♦10-2 ♣9-8-6
Both East's should end up in 3NT, but will lose the first 7 tricks with East 1 as dummy.
But with the ♥ Ace, West will immediately clear 9 tricks against a ♥ lead, and 10 tricks against a ♣ lead.
You need to constantly upgrade hands with Aces, and downgrade hands without any Aces. One system reduces the point count by 1 for hands with no Aces.
Just how important 10's and 9's?
Hand A ♠K-6-4 ♥A-Q-6-4 ♦Q-J-4 ♣Q-J-3
Hand B ♠K-10-8 ♥A-Q-9-4 ♦Q-J-8 ♣Q-J-9
Hand C ♠K-10-9 ♥A-Q-10-9 ♦Q-J-10 ♣Q-J-9
Each hand has 15 HCP's, but many experts would avoid opening 1NT with Hand A, would pass a Responder bidding 2NT with Hand B, and would raise to 3NT with Hand C.
Now will both these hand make 3NT on a ♥ lead?
West ♠K-J-3 ♥A-6-4 ♦A-10-6-3-2 ♣K-5
East 1 ♠Q-6-5-2 ♥K-7-3 ♦J-7-5 ♣A-J-4
East 2 ♠Q-10-9-5 ♥K-10-9 ♦J-9-8 ♣A-J-10
Each East has 11 HCP, but East 1 will go down. East 2 will normally be able to establish the ♦'s and the intermediaries in the other suits will make it difficult for Opponents to establish a suit quickly.
One suggestion is adjust the HCP of a hand by looking at the number of Aces and Kings and subtracting the number of Queens and Jacks, and altering the HCP if the difference is bigger than +2 or -2.
East 1 ♠Q-6-5-2 ♥K-7-3 ♦J-7-5 ♣A-J-4
East 2 ♠Q-10-9-5 ♥K-10-9 ♦J-9-8 ♣A-J-10
Above we saw how important 10's and 9's can be, so is K-Q-J even more important that its 6 HCP's?
West ♠K-Q-J ♥A-10-8 ♦K-9-7 ♣Q-8-6-4
East ♠10-9-7 ♥K-Q-J ♦A-6-4-2 ♣9-7-3
Both east and West will consider K-Q-J as 6 HCP's, and the bidding is a simple 1NT - 3NT, or is it? They will go make 7 or 8 tricks. The reality is that K-Q-J-x is worth 6 HCP's and K-Q-J-x-x is worth even more. Honours are worth more in long suits, and the above hand is flat with no 5-card suits. Bothe should have downgraded their hands by 1 HCP, and ended in a contract of 1NT.
Short honour combinations such as K-Q, A-K, Q-x, A-Q, A-Q-J, … are worth less than their HCP's would suggest. But these combinations, as well a K-Q-J, should be upgraded if they are in partners suit.
Some plays subtract a point for doubletons of the type A-J, K-Q, K-J, Q-J, Q-x, and J-x, as well as honour singletons (note A-K and A-Q are excluded from this list).
Warning signs can be multiple, consider this hand played in an international tournament.
West ♠K-Q-J ♥Q-9-7-4 ♦A-Q-J ♣Q-J-5
East ♠10-6 ♥K-J-5 ♦10-8-4-3 ♣K-8-4-2
It looks like West has 18 HCP's and 1♣ - 1NT - 3NT looks credible. It would go down against a lead from a 5-card ♠. What actually happened was that Opponents intervened with a 1♠ - 2♠ over the opening 1♣. One E-W took the 200 penalty points (2 down vulnerable), but despite the warnings the other three tables still bid to 3NT and predictably went down. The warning signs are there, K-Q-J and the A-Q-J should be downgraded, no 5-card suit to exploit, a poor 4-card suit, and you would expect to see two Aces in an 18 HCP hand. And alternative is to heed the warning signs, downgrade the K-Q-J and the A-Q-J, open 1NT, and East will Pass.
Are fitted honours good?
Combinations such a Q-7-3 are weaker than they look, except when they are in a suit mentioned by partner.
West ♠A-8-6-4 ♥A-K-8-6-4 ♦8-6 ♣A-2
East 1 ♠K-Q-4-2 ♥9-7-3 ♦Q-7-3 ♣9-6-4
East 2 ♠K-Q-4-2 ♥Q-7-3 ♦9-7-3 ♣9-6-4
Here we have West opening in ♥ and over East's 1♠, West invites with 3♠. What does East do? East 1 will certainly refuse the game invitation. But East 2 should upgrade the ♥Q in the first suit of Opener, and accept the invitation to bid game 4♠ (and made). It's worth noting that even a ♥Q-7 is worth upgraded.
West ♠A-K-10-3 ♥8-6-2 ♦A-K-9-6 ♣Q-2
East ♠Q-J-9-4-2 ♥9-7-5-3 ♦Q-3 ♣A-6
West would normally open a strong 1NT and the final contract would be 4♠. But if they were playing a weak NT, west would open 1♦, East would reply 1♠, and West would invite with 3♠. Would East accept? Swap ♦Q and the ♥9, would East still accept? In the first case the ♦Q is fitted, East accepts, and they bid and make 4♠. In the second case, the ♥Q would not be fitted, and the invitation should be refused, i.e. 3♠ makes, 4♠ goes down.
What's the value of touching honours?
Is K-J-x-x better than Q-J-x-x, apart from the extra 1 HCP? Is K-J-x-x worth that extra point? Touching honours, with at least a third card, are valuable.
A simple example, if you are holding K-x-x and your partner Q-x-x you will make 1 trick, whereas holding K-Q-x in front of x-x-x, you have a 50% chance of making two tricks if the Ace is sitting on your right.
West ♠A-9-4 ♥A-8-3 ♦J-7-5-3 ♣K-10-5
East 1 ♠K-J-7-6 ♥K-9-2 ♦A-9-6 ♣Q-7-4
East 2 ♠Q-J-7-6 ♥K-Q-6 ♦K-Q-9 ♣9-7-4
Both East's have 13 HCP's, and you might think East 1 looks better because it has an honour in each suit. However, East 1 would need a miracle to make 3NT, whereas East 2 has a fighting chance because of the touching honours K-Q have each found a touching honour with West.
So combinations such as K-Q-x-(x), Q-J-x-(x) and J-10-x-(x) are superior to A-J-x-(x), A-Q-x-(x), and K-J-x-(x). Touching honours are twice as likely to find a touching honour with partner. In the same way Q-J-10-x is better than Q-J-9-x. And remember K-Q-x-x is better than K-Q-x, because you could find it sitting in front of A-J with partner, so below Hand A is far better than Hand B.
Hand A ♠K-Q-7-6 ♥Q-J-5-3 ♦A-9-6 ♣7-4
Hand B ♠K-Q-7 ♥Q-J-5 ♦A-9-6 ♣9-8-7-4
One suggestion is to reduce the value of a Q or J when not accompanied with a King or Ace. The also noted that a doubleton Q-J was not worth 3 HCP's.
How important are long suits with productive honours?
The message is long suits are good, and long suits with honours are better. Which of the two hands below is better?
Hand A ♠A-K-9-7-4 ♥A-Q-8-6 ♦7-6-4 ♣8
Hand B ♠A-8-5-4-3 ♥Q-8-6-4 ♦K-J-8 ♣K
Obviously Hand A, because the honours are working, able to create winners in the long suits. If you opened with 1♠, and partner raised to 3♠, you could bid game with Hand A, but should Pass with Hand B.
Hand A ♠Q-J-6 ♥K-J-2 ♦A-9-3 ♣10-9-4-2
Hand B ♠Q-7-6 ♥K-J-2 ♦A-9-3 ♣J-9-4-2
With Hand A you could upgrade your 11 HCP's and invite with 3♠ over an opening 1♠, whereas with Hand B you would be wise to downgrade your hand, and bid 2♠ over an opening 1♠. The position of the Jack makes all the difference. Just counting 1 HCP for a Jack is not good enough, it has to be the right Jack in the right place.
Some players add an additional point for a good 5-card suit, and an addition 2 points for a good 6-card suit, and even 3 points for a long suit with three honours from five, and headed A-K.
How important is the 9th trump?
The 9th trump is possible one of the most important reasons to adjust a point count. It changes a 5-3 fit into a 5-4 fit or even a 6-3 fit, and often a 4-3 into a 4-4 fit. But the adjustment is not always in the same direction, a 5-3 might be enough, and upgrading because of a 5-4 might not produce an extra trick.
Have a look at this hand from an international tournament.
West ♠K-10-8 ♥10-5-2 ♦7-6-5 ♣A-K-J-9
East ♠A-Q-J-9-4-3 ♥A-6-4 ♦- ♣Q-10-8-3
What is best contract? Some made 4♠+1, some went down 6♠-1. However, there is 7♣.
Is this not all about "shape"?
Clearly long suits are an advantage, because they can be a source of tricks. Plus long suits means there are short suits, and a source of ruffs. So the shape 4-3-3-3 is bad in both senses.
Hand ♠K-7-5 ♥J-10-9 ♦A-9-8 ♣K-J-8-7
This had might look like 12 HCP's, but it is flat, and in terms of trick potential it is weak. Often the shape 4-3-3-3 is worth a point deduction.
Here is an international competition hand.
West ♠J-6-2 ♥Q-9-5 ♦A-K-8 ♣Q-8-6-4
East ♠A-K-Q-10-5 ♥J-7-6-3 ♦Q-3 ♣9-3
Should West open with a balanced 12 HCP? It's a poor hand with just two sure winners, plus do you open 1♣ with this? One table did open a weak NT, and East end up in 4♠-1. A simple Pass at the other table gave them a decent swing.
Does it matter who plays the hand?
Yes and no, because in most cases the partnership does not have the choice.
But have a look at this hand…
West ♠A-8-7 ♥Q-7 ♦K-J-10-7-2 ♣A-9-8
East ♠K-9-4 ♥A-5-4 ♦Q-8-5 ♣K-6-5-2
Firstly the ♥Q-7 does not look that appetising, should West downgrade the hand. If West opens 1♦, East will end up playing 3NT. The lead will be a ♥ through ♥Q-7 with North holding a 5-card ♥ by K-J and (naturally) the ♦Ace. Result 3NT-1. The argument is that with Q-x its usually better to be declarer in a NT contract. So West can upgrade or downgrade their hand to try to ensure who plays the contract. Here West actually upgraded their hand and opened 1NT, and ended with 3NT+1.
The advice is that with an honour second (A-x, K-x, Q-x) or A-x-x, its better to be declarer in NT.
What have we learned so far?
Downgrade a hand because:-
- It's a flat 4-3-3-3
- It doesn't have an Ace
- It doesn't have a long suit
- It doesn't have intermediaries, e.g. 10-9-8's
- It doesn't have touching honours
- The honours are not productive, i.e. not in your long suit
- The honours are not "fitted", i.e. they are "lonely".
Upgrade a hand when:-
- It has an Ace
- It has a long suit that will make tricks
- it has a useful 9th trump
- It has good intermediaries
- The honours are working for you, e.g. touching, in the long suit, and/or "fitted".
Try this…
Your Hand ♠K-6-2 ♥Q-J-5 ♦Q-7-6-3 ♣K-5-2
Your partner opened 1♣, you replied 1♦, and they bid 1NT (12-14 HCP's). You have 11 HCP's, do you invited with a 2NT? No, even if your partner has a maximum 14 HCP's, your hand has no long suit, no intermediary cards, and it's certain that some of honours will not work for you. Partner might have one or two hands that could be enough for 3NT (e.g. good 5-card ♣, a finesse that works, and a useful lead), but there are a lot of 14 HCP hands that won't have that essential good 5-card ♣, etc. Below is your partners hand…
Partners Hand ♠A-9-4-3 ♥A-10-4 ♦A-9-2 ♣Q-8-3
Try this…
Your Hand ♠K-Q-6 ♥K-6-4-2 ♦Q-J-7 ♣7-5-3
Partner opened 1♦, you replied 1♥, and they bid 1NT (12-14 HCP's). Your hand is flat, your ♥'s are weak, your honours K-Q and Q-J are in short suits, you have no intermediaries, and the ♣'s are a waste of space. What could you bid? An invitational 2NT? Try to imagine the kind of hand you would need to find with your partner. And imagine all the hands you are likely to find with your partner, e.g. flat, 14 HCP's (they could have only 12 HCP's), some honours not working for you,… Best to downgrade your hand and Pass. Here is your partners hand, not bad 14 HCP's and a couple of 10's, …
Partners Hand ♠A-J-10 ♥7-6-5 ♦A-K-10-8 ♣Q-8-7
Lucky you passed, you should be very happy with 1NT, and ecstatic with 1NT+1, but you could also go down.
Often a hand assessment is a mix of +'s and -'s. How would you assess this hand…
Your Hand ♠9-7-5 ♥A-7-5 ♦A-K-64 ♣A-6-5
Your are 4th in hand after 3 passes, and you are playing a strong NT. What do you bid?
Does all this matter when you have lots of points?
Imagine you have the following hand…
Your Hand ♠A-K-7 ♥A-J-10-9-7 ♦A-J ♣A-J-10
What would you open with this 22 HCP's? Some might say 2NT (20-21 HCP), but there is a bid "2♣-2NT" which is a super NT indicating 22-23 HCP's. There is a good chance that partner will raise to 3NT, or even beyond. When you have lots of HCP's, do you need to adjust your points up or down?
With a strong hand, there is a good change that it will both bid and play the game contract, often in NT, or even in a slam. So more than ever, long suits will be the source of additional tricks. And this is true for both Opener and Responder.
Hand A ♠5 ♥8-5-4 ♦K-Q-9-6-4-3 ♣8-7-3
Hand B ♠5-4 ♥8-5-4-3 ♦K-Q-9-6 ♣8-7-3
Your partner opens 1♣, do you bid? With Hand A it is worth a 1♦, but with Hand B it might be better to Pass. Let's say the bidding is 1♣ - 1♦ - 2NT, do you raise to 3NT? Yes with Hand A, no with Hand B, simply on the basis of suit length that could be a source of additional tricks. Those extra two cards in ♦'s makes all the difference.
More so than ever, a singleton or void can make all the different between game and slam.
West ♠A-Q-8-6-5-3 ♥J-3-2 ♦A-3 ♣A-K
East ♠K-7-4-2 ♥K-9-8-5-4 ♦K-10-7-4 ♣-
West has a powerful hand, but will still open 1♠, and East could bid a splinter. But if West had a minimum opening, they could still go down in 4♠. What does East do? One possibility is 1♠-3♠, but is East not undervaluing the hand, perhaps 1♠-4♠, but that could still be undervaluing the hand (does East not have 15 DH?). How about 1♠ - 2♥ - 3♠ - 4♣ (control) - 4♦ (control), … could they stop in 4♠, or 5♠, or would they end up in 6♠? A ♥ lead past the ♥K to the A-Q and a ruff back, means East-West makes only 10 tricks. The problem was that East was overvaluing the void without knowing how useful it would really be. Clearly East should upgrade the hand, but only to a limit bid.
Adjusting the point count is really a problem of assessing the positives and negatives in a hand. Consider the following hand…
Hand ♠9-7-5 ♥A-7-5 ♦A-K-6-4 ♣A-6-5
You have 15 HCP's, you have the Aces, and a nice 4-card suit. But the hand is flat, and lack intermediaries. Would you open 1NT? Remember flat hands are worth 1 HCP less!
Would you open 1NT after Partner had passed? Certainly not, an opening 1♦ is far more reasonable. Lets assume you find a Partner with 9 HCP and a 5-card ♠. At best you make 3♠, at worst you struggle to make 2♠. Had you started with 1NT, you would have ended in a costly 4♠.
Now consider this hand…
Hand ♠J-8-4 ♥Q-7 ♦K-Q-9-4 ♣A-K-10-6
Again 15 HCP's, but this it is not a flat hand and the points are in the two 4-card suits, plus you have some reasonable intermediaries that might tie together with partners intermediaries. And as mentioned above you have the famous Q-x. So this hand is worth an opening 1NT.
Re-evaluating Openers hand
The starting point is that Opener only considered HCP's, and excluded short-suit points, but includes any points for suit length. The idea is to add points for trump suit length and suit quality. The suggestion is to add a point for a 6+ trump suit, 1 point for each trump card above 5. In addition a point can be added for a 4-card or 5-card side suit. And in addition 1 extra point for 2 (or 3) doubletons, 2 extra points for a singleton, and 4 extra points for a void. As an example …
Hand ♠A-K-4-2 ♥K-Q-6-3-2 ♦A-K-10-9 ♣-
Opening 1♥ Partner replies 3♥ (10-12 Dummy Points). This had would now be re-evaluated as 19 HCP' plus 1 point for trump length, plus 1 point for suit quality, plus 1 point for a 4-card side suit, plus 4 points for the void, for a total = 26 points. With the points in Dummy, enough for a slam bid.
Re-evaluating dummy
Often it is clear which hand will be the Dummy, and that player needs to re-assess their hand. This could be because Opener bid a major, and (future) Dummy has 3-card support. Dummy needs to re-evaluate the hand based upon becoming dummy.
Some players add a point for a doubleton, 2 points for singleton provided they hold at least 4 trumps, and for a void they add point equal to the number of trumps in their hand. The arguments here is to never count points for doubletons, singletons, or voids, before knowing what the suit contract will be. Try these hands…
Hand 1 ♠A-Q-6-7 ♥8-7-6 ♦A-K-10-4-3-2 ♣-
Hand 2 ♠10-9-8-6 ♥K ♦7-5-3 ♣Q-9-4-3-2
Hand 3 ♠10-2 ♥J-6-4 ♦K-Q-J ♣K-Q-10-9-8
Hand 1 has 13 HCP + 2 points for the good honours + 1 point for the ♦ suit quality = 16 points. To which you could add 3 points for the void if Partner plays in ♥'s.
Hand 2 has 5 HCP plus 1 point for the length in ♣'s, minus a point for the singleton King = 5 points. To which you could add 3 points for that singleton if Partner plays in ♠'s.
Hand 3 has 12 HCP plus 1 point for length in ♣'s, plus 1 point for the quality of the n ♣'s. The presence of 2 Q's and 2 J's is a negative, but is off-set by the presence of two K-Q. You could add a point for the doubleton ♠ if Partner was playing in ♥'s.
Most players look to re-evaluate Dummy and add points for doubletons, singletons, and voids (1, 3 and 5 respectively). But this only counts if Dummy has the trumps to ruff.
Playing Tricks
Playing tricks is a useful alternative way of hand assessment, in particular for opening weak-2 bids and pre-empts. Consider…
♠6-4 ♥A-K-Q-J-10-5-2 ♦6-4 ♣J-7
We presume that long suit(s) break evenly in the other three hands, and we can see 7 playing tricks. However with …
♠K-4 ♥A-K-Q-J-10-5-2 ♦Q-4 ♣K-J
The Kings and Queens must be worth something. K-x is usually considered as a ½ playing trick, A-Q-x as 1½ playing tricks, etc. A suit such as ♥K-J-8-6-5-2 would be worth 3½ playing tricks.
Playing tricks are more difficult to assess in stronger hands, where it would be wrong to give a ½ playing trick to K-x, knowing that partner might well be holding honours in the same suit, e.g. ♥K-J-8-6-5-2 might be worth 3½ playing tricks, but if partner holds ♥Q-x, you could be looking a 5 playing tricks. So strong hands should not add playing tricks, leaving the weaker partner to assess their playing tricks in support of the stronger partner. And remembering that partner needs entries so that declarer can take the finesses, otherwise a A-Q-x is only worth 1 playing trick.
In the above description, length in trumps and shortness in suits both score additional points, yet often a ruff is only using a trump that Declarer had already counted as a winner. They do not create additional tricks, even if they may be essential to the contract. Other players highlight the value of the long side suit as a way to find additional tricks. A good 4+ card side suit can be very valuable.
Another point noted was that an aggressive raise of Openers suit may reduce the risk of an intervention, and equally allows Opener to better compete with Opponents.
Honours held in suits mentioned by the Right-Hand Opponent are more valuable than honours in suits mentioned by the Left-Hand Opponent.
A final comment was that a partnership should flatter their hand if they are likely to be defending, and be more cautious when they are likely to take the contract.
Controls
Sometimes it is difficult to evaluate the game or slam potential of a hand, e.g. should you Pass or bid game or even a slam? One way is to look at 'controls', e.g. the Aces and protected Kings that correspond to a particular HCP. If a player has 5 HCP then they should hold an Ace or King, if not the hand is 'weaker' than 'average'. Many experts attribute 2 control points to an Ace and 1 control point to a King. Hands with 5 HCP and only 1 control point, and hands with 7-8 HCP and only 2 control points are considered poorish hands.
Things start to look interesting with 10 HCP and 3 control points, with 12-13 HCP hands should have 4 controls, 15 HCP expect 5 controls, 17-18 HCP expect 6 controls, and with 20 HCP hands should have 7 controls. You might like a hand holding A-K-x and another K-x-x, but not a hand holding A-x, plus 2 Queens and 2 Jacks is different suits.
However the reality is that analysing 1,000's of real world bridge hands the correlation of controls and trick winning is not that good. The use of controls is probably more useful in specific situations rather than as a general principle.
Another equally useful approach for these 'boarder line' hands is to look at the presence or absence of specific negative features that would reduce the value of a particular HCP count. These are:-
Honour doubletons K-Q, K-J, Q-J. Q-x, J-x unless in partners suit - reduce by 1 point from the HCP count.
Honour singletons (exempt the singleton Ace).
Honours in opponents' suit when deciding to support partner's suit (these points could be useless), and in particular honours in suits shown by your Left Hand Opponent (they are sitting 'over' you).
There are also specific distributions that enhance hands and support a more 'aggressive' bid, namely:-
- Two or three honours in long suits, or better still honour sequences in long suits - add 1 point to the HCP count.
- Honours in partner's suit when deciding to support it.
- Honours in own suit when deciding to overcall.
- Two or three intermediate cards in a suit (8, 9, 10) especially if headed by honours.
- Honours in suits shown by the right hand opponent (you are sitting 'over' them).
And many players like to open the ♠ suit whenever possible to make overcalling more difficult.
Assessing a 'boarder line' hand is also about the defensive strength of a hand. Good defensive values include:-
Honours in shortish side suits, e.g. K-x-x.
Honours and/or length in opponents suit.
Lack of honours in your own suit.
Players might find it better to play a contract rather than defend if they have an abundance of honours and length in their own suit, and a lack of defensive values. Again the decision will also be affected by the vulnerability.
There are some 'quick fixes' to assess the opening value of a hand, e.g. the 'rule of 20' or "open if the HCP plus the number of cards in the two longest suits add to 20 or more". Another way is to add the number of cards in the 5+ length and the number of honour cards in the same suit (Ace down to and including the 10). With 7 open at the 1-level, with 8 open at the 2-level, and with 9 open at the 3-level.
Losing Trick Count
A technique which I personally like to use to assess 'boarder line' hands (and this can be when deciding to bid, over-bid, to support partner, to Pass, ... as well as to bid game or even look for slams) is the losing-trick count. This is used when a partnership has found a trump fit. The question is often, do I raise, bid game, stop, invite, ....? It does not replace point count but does provide a useful second opinion, in particular when shape and fit are more important than HCP's and you need to decide how high you can bid.
The idea is to weigh shape and fit rather than just point counts. The player should look only at the top 3 cards in each suit. Then evaluate losers in each. If you have a void, you have 0 losing tricks. A singleton (other than an Ace) is 1 losing trick. An Ace and King doubleton is 0 losing trick, whereas A-x, K-x or K-Q is 1 losing trick, and naturally something like Q-x, J-x or x-x is 2 losing tricks. So clearly with 3 cards such as A-Q-x or K-Q-x you have 1 losing trick. This gives your losing trick count for the hand. If you open you are presumed to have 7 losing tricks, so this helps you decide to open or Pass with certain boarder line hands. If you partner also has 7 losing tricks he knowns that 7+7=14, subtract from 18 leaves +4, so you can bid up to level 4 or game in a major. If your partner has 8 losers they would jump to the level of 3, e.g. 18-(7+8)=3. and with 9 losers you simply raise to 2, e.g. 18-(7+9)=2. And of course if you only have 5 losers then 18-(7+5)=6, a slam is certainly possible. Some people count to 18 and others to 24 but the result is the same, e.g. 24-(7+7)=10 total tricks.
Clearly as opener if your partner supports your suit you can then 'count' the number of losing tricks, and you can invite or even raise to game as required.
The key numbers are:-
7 expected losers when opening with 13-15 HCP
4-5 expected losers when opening with 20-22 HCP (2♣ or 2NT)
3-4 expected losers when opening with 22+ HCP (2♦)
6-7 expected losers when pre-empting at level 3 (vulnerable/non-vulnerable)
Take-out double at the 1 level means 6-7 losers
Take-out double at the 2 level or above means 5-6 losers
Simple overall means 6-8 losers
9 expected losers when responder shows 6-10 HCP
8 expected losers when responder shows 10-12 HCP
7 or less losers when responder shows 13+ HCP
An invitation by Opener (16-17 HCP) means 6 losers
Raising Responder to Game (18-20 HCP) means 5-6 losers
One key message, don't open with 11-12 HCP and 8 losers, instead of the 7 needed.
An analysis of 1,000's of real world bridge hands shows a good correlation between counting losers and winning tricks. It's good, but not that good.
There are more complex loser counting systems, but I find this one is simple and provides help in deciding about boarder line hands. Some experts think that this count system undervalues Aces and overvalues Q-x or singleton Kings.
One comment is that the loser trick count does not replace point counting, but it helps in particular where shape and fit are more important than HCP's, and when deciding "how far to go". As I use it, it's a "second opinion".
An interesting suggestion was to adopt a "Two Dimensional" analysis using both point counting and losing trick counting. It was suggested that point counting was better balance and loser trick counting more adapted to aggressive bidding based upon distribution, you might have only 11 HCP, but you could have 7 losers (i.e. enough to open). So each point range there is a "bad", "average", and "good" range of loser tricks.
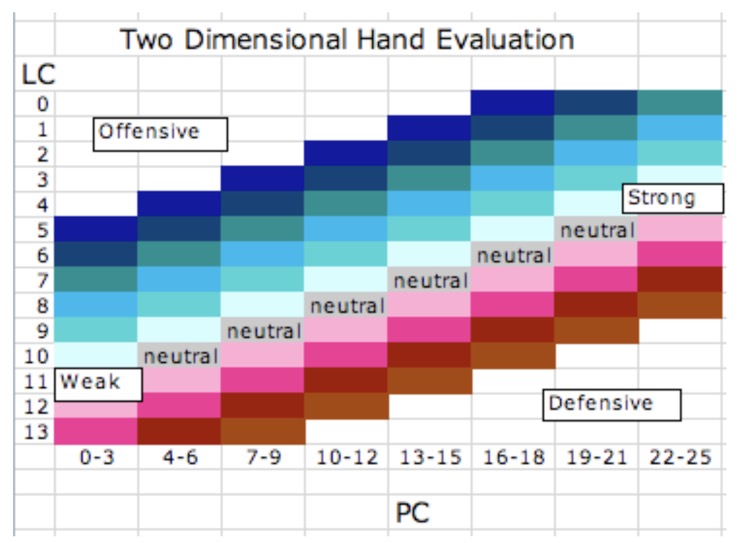
As an example. Opener might have 13-15 HCP, and 7 losers, this would be neutral. It is possible that Opener might have only 5 losers which would suggest aggressive bidding, however its possible that Opener has 9 losers, suggesting a poor flat hand.
Total Number of Tricks
In situations where partnerships have a fit but are competing with their opponents it is sometime difficult to decide to make an additional bid or just Pass. A simple rule is that a partnership will make (more or less) the number of tricks corresponding to their combined holdings in trumps (this is the so-called T.N.T. or Total Number of Tricks). This is particularly useful when a partnership has made a weak-two or weak-three opening bid or overcall, indicating 6, 7 or even 8 cards in a particular suit. If the partner has a weak defensive hand they can bid to the level of the combined holdings in their suit, e.g. holding a total of 9 cards in their suit they bid to the 3-level. Clearly they need to be careful about the vulnerability at the table.
Hybrid
In a workshop in early 2019 hosted by Milan Macura there was a suggestion to use different hand assessment schemas for different types of hands.
You should use high-card points (HCP) for balanced hands which are mostly likely to be played in NT.
You should use high-card points (HCP) plus distributional points (my DH) for irregular or semi-balanced hands where the contract might be in a suit.
And you should use losing trick count for truly unbalanced hands.
This is just a marker for this hybrid approach, which is developed in more detail on a separate webpage.
Shape - hand evaluation in one word
A lot of players will stop once they have counted their high-card points (HCP) and adjusted for a long or short suit. But in fact it's just the start. With DH calculated the player is on the first rung of the ladder.
Hand evaluation is in reality all about shape. This last section is the longest on this webpage, and in many ways one of the most important. So take your time, read carefully, and maybe it will change the way you evaluate your bridge hands. But a word of warning is in order, you will need to know how to play your cards after you have won the auction.
Shape tells us that in a suit contract a doubleton is essential, and two is even better if it comes with a 6-card trump suit. In No Trump 4-4-3-2 is better than 4-3-3-3, and 5-3-3-2 is also an even better shape for No Trumps provided the 5-card suit is a minor (although most experts will also play No Trumps with a 5-2 in a major and semi-balanced distribution).
Shape tells us that honour combinations in the same suit are more powerful than the two honours sitting in two different suits. A simple Q-x-x-x will add almost nothing to a contract if it's not in trumps, and a King in a side suit might not be worth much more. But a K-Q-x-x is an entirely better story even opposite x-x-x with Partner. Honours in long suits are worth more than the same honours in short side suits, simply because it will be easier to establish the long suit. Stating the obvious, K-Q-x-x in front of x-x, is better than x-x-x-x in front of K-Q.
Shape tells us that intermediate cards, 10's and 9's, can change completely a hand, particularly if they are sitting under one or more honours, A-J-10-9 is great sitting in front of x-x-x, or would you prefer A-J-x-x in front of x-x-x?
Shape tells us that side suits are often essential to making a contract, in particular when playing weak hands. Shapes such as 7-3-3-0 or 7-4-2-0 are far superior to 7-2-2-2. Many experts prefer hands as unbalanced as possible, and average players don't play unbalanced hands very well.
Shape tells us that honours in your hand are more valuable if they are in a suit bid by Partner. They are also more valuable if they are in the suit bid by your right-hand opponent (RHO). Honours in unbid suits are less interesting, and honours in suits bid by your left-hand opponent (LHO) are also of less value. But think a bit more. If you are holding a singleton or doubleton in opponents suit, then what you want is for Partner to be void in honours in that suit as well.
Shape tells us that if your Partner has bid a side suit, then holding support in that suit is good, but equally being shorted in that suit can be useful if your trump holdings are sufficient. If you know that Partner is short in the opponents suit, the holding K-J-x-x in that suit is not likely to be useful, but holding x-x-x-(x) is a good thing. Firstly, points are not wasted on a weak suit, and secondly Partner will be able to ruff your losers. This is one reason why experts play Splinter bids, it shows immediately a fit with no wasted values.
We are closing this webpage with a discussion of shape, and a series of examples and test questions.
Example 1: ♠6-3 ♥K-8-3 ♦Q-J-8-4 ♣A-Q-J-5
Example 2: ♠Q-J ♥A-Q-J ♦K-8-4-3 ♣8-6-5-3
In these two hands the honour cards are the same, and the distribution is the same. However one is superior to the other. The first example has its honour cards better protected and they are in the 4-card suits which might make it easier to establish extra length tricks. The honours in the short suits in the second example may still win tricks, but they probably will not create extra length tricks.
Example 1: ♠9-8-6-4-3 ♥A-Q ♦K-Q ♣J-8-3-2
Example 2: ♠A-Q-9-8-6 ♥4-3 ♦3-2 ♣K-Q-J-8
Same HCP and distribution, but the 'quality' and playing shape are totally different, and example 2 is by far the better hand with all the honour 'pulling their weight'. In the example 1 the hand does not provide much support for Partner bidding a red suit, and even with a fit would require honours and length from Partner in the black suits. Some players would see more defensive strength in example 1, and would not open with this hand. In example 2 the hand is certainly worth opening because there could be a chance of game if Partner has support for ♠ and a decent 11-12 HCP.
Example 1: ♠K-Q-8 ♥Q-J-5 ♦K-Q-10-9-2 ♣8-5
Example 2: ♠A-Q-8 ♥Q-J-7 ♦10-7-6-4-3 ♣A-9
These two hands have same number of HCP and the same distribution, but does that make them the same? In a major or No Trumps it's going to be difficult to establish additional tricks in the long ♦ in example 2, whereas in example 1 Declarer would have a fighting chance.
So what should we be looking for?
Positive features are:-
Holding several intermediate cards, 10, 9 and 8
Have intermediate cards in the long suits
Having a 5-card suit or two 4-card suits
Honours in the long suits
Touching honours
Length in the majors
Holding Aces
Negative features are:-
- Lack of intermediate cards
- Suits with unsupported honours, or two honours not touching
- The 4-3-3-3 distribution is the worst one you can be dealt
- Honours 'lost' in short suits, e.g. Q-x
- Too many Jacks that may not actually serve any useful purpose.
You will see many of these advantages and disadvantages mentions in the below section on controls.
Let's look a bit more at specific shapes, i.e. distributional patterns.
4-3-3-3 is disliked by many players because it provides no ruffing potential and no long suit potential in No Trumps.
4-4-3-2 is better than 4-3-3-3 in that it offers potential to find a 4-4 fit in a major, or a 9-card major suit if Partner opens.
5-4-2-2 is a semi-balanced distribution, but could be considered balanced if the honours are in the short suits, and in any case it permits the player to consider bidding in two different suits. With this type of distribution the hand is considered stronger if the honours are in the long suits.
5-4-3-1 is unbalanced and is better than 5-4-2-2. The unbalanced distribution offers 2 possible trump suits in the majors, support for a bid in a 3rd suit, and with ruffing potential. The semi-balanced shape 5-4-2-2 just offers two possible trump suits. Obviously 5-4-4-0 is even better.
6-5-3-0 is better than 6-3-3-1, which is better than 6-3-2-2.
7-3-3-0 or 7-4-2-0 is better than 7-3-2-1 and the worst is 7-2-2-2.
Example 1: ♠J-6-3 ♥A-K-Q-J-10-9 ♦Q-4 ♣8-3
Example 2: ♠K-J-3 ♥Q-J-10-9-6-3 ♦A-Q ♣8-4
One word of warning. It is possible to be too rich in a long suit. Which hand do you prefer? Example 1 will win you 6 tricks, but nothing else, and in game Partner will need to bring you 4 tricks. With 3-card support you don't need the Jack and the Queen is not really needed 50% of the time. It would be much better to have those 3 HCP somewhere else, better still as a King. In example 2 you have the same HCP and the same distribution but two of the side suits have useful honours. Yes, you might have given up the top honours in trumps but you should make that up because your trumps are solid and you will almost certainly find a good side suit with Partner. We should not go too far in this logic, the trump suit should be solid enough to play with 2 or 3 small cards with Partner, e.g. yes to ♥Q-J-10-9-6-3 and no to game with only ♥Q-8-7-5-4-3.
Here are some tests about shape and hand evaluation
Test 1: Your Partner opened 1NT, with ♠A-Q-4 ♥8-5-3 ♦A-J-10-9-7 ♣10-2 you bid what?
Test 2: With ♠A-J-10-8-6 ♥K-Q-10-7-4 ♦8-6 ♣3 do you Pass or open?
Test 3: Your Partner has opened 1♠, holding ♠5 ♥Q-8-4-3 ♦K-8-5 ♣K-J-5-4-2 what do you bid?
Test 4: Your Partner has opened 1NT, holding ♠J-8-6-4 ♥K-8-3 ♦A-J-2 ♣Q-9-5 what do you bid?
Test 5: With ♠K-Q-J-8-7-6-5 ♥8-2 ♦J-10-9-8 ♣- what do you bid?
Test 6: With ♠K ♥Q-J-6-3 ♦A-J-8-7-5 ♣Q-8-2 what do you bid?
Answers:-
Test 1 - This is a good 11 HCP (8-losers) which could bring 5 or 6 tricks to Partner, bid 3NT.
Test 2 - With 10 HCP (6-losers) but great shape with honours in the long suits and including 10's, bid 1♠.
Test 3 - This hand has 9 HCP (7-losers) but has a lot of negative features, split honours in ♣ and an exposed K and Q, a bid of 1NT is the only option.
Test 4 - This hand has 11 HCP (9-losers) but has lots of negatives, a flat distribution 4-3-3-3, exposed honours, no intermediate cards, it could bring 3-4 tricks to Partner or just 1 trick. Some players might bid 3NT, other might Pass, and others might bid 2NT. Expert opinion is to Pass.
Test 5 - With 6 HCP (6-losers) and a 7-2-4-0 shape, this is ideal for a pre-empt, but at what level? Let's say that both pairs are vulnerable, does that help? This hand is too strong and yet still weak. Ideally you want to bid, take the contract and not be doubled. The only bid that has that chance is 4♠. If Partner has 0 points you have 6 winners in ♠ and a winner in ♦, so down 3, against opponents who have 34 HCP.
Test 6 - You have 13 HCP (7-losers), but it is a poor opening hand, and should be downgraded because of the singleton King. Downgrading this hand means 'Pass'. If you open 1♦ you have nowhere to go except 2♦. This hand has a good shape and a lot of bidding options should Partner open or intervene.
Game try
Above we saw that shape is important in deciding to bid or Pass. But it is equally important in understand if you should bid game or accept a part-score.
Opener bids 1♥ and Partner responds 2♥, what does Opener do now?
Test 1: ♠J-3 ♥A-Q-J-7-4 ♦A-Q-10-8-6 ♣5
Test 2: ♠5 ♥A-Q-J-8-6 ♦10-9-6 ♣A-K-Q-3
Test 3: ♠Q-J-6 ♥A-K-J-9-2 ♦K-3 ♣Q-8-4
Test 4: ♠Q-8-4 ♥A-Q-8-3-2 ♦A-7-4 ♣K-5
Test 5: ♠K-5 ♥A-Q-J-10-8-6 ♦J-10-2 ♣9-7
There is a nice rule that was mentioned in the article I'm using for this last part on shape. The attribution is to Tony Forrester, and is often called the 'Two Card Rule'. Sit back and think, Partner is promising 3-card support and 6-9 or 6-10 HCP. What can we expect from Partner in an ideal world? Let's say 2 good cards, maybe an Ace and Queen, or two Kings. Some players might pump that up to 7 HCP and expect an Ace and King. Clearly Partner could be supporting Opener with rubbish, but good shape, who knows.
In any case if those two good cards are not enough for a chance of game, then Opener should 'Pass'. Let's face it you might want to 'invite' but if you can't 'see' game even with those two ideal cards, then what's the point of inviting? This is an important concept, if under ideal circumstances Partner can't be holding what you need why continue? Even if you have 'extras' your Partner can't perform miracles, they just can't have more than the ideal.
Now if Opener has a good shape, then it might be worthwhile telling Partner. What Opener will want is that the honours in Partners hand fit well with a long side suit, and if they are opposite a singleton or doubleton they will be less valuable. The standard approach is to bid a long (4-card) side suit to help Partner judge how much waste they have.
How to judge 'waste'? Three of more cards with no top honours in a suit is a bad holding, and Partner should downgrade their hand. Partner will upgrade their hand with less than three losers in that suit. This could be with an honour heading 4 cards in the side suit. Or it could be with ruffing potential on that side suit, provided Partner has a 4-card support in trumps.
So let's have a look at our test hands. Answers:-
Test 1: With a hand of 15 DH and only 5-losers, a game is certainly worth a try. A bid of 3♦ will enable Partner to upgrade their hand. Support in ♦ would be great, and since Opener is short in black cards an Ace or King in ♠ or ♣ could be very valuable, but minor honours in black suits will be worth little or nothing.
Test 2: With 19 DH and only 5-losers, again game looks a good option. Some players might say a bid of 3♣ is a good idea (like in Test 1 above). But let's face it, Partner will have bad cards in ♣'s and could even be discouraged and not bid game, but a bid of 3♦ might do the job since you are going to need a winner there. Of course in a simple bidding model, Opener will just bid game on the basis that there is a good chance that opponents will not be able to run 3♦ winners and the ♠Ace. And Opener bidding 3♦ might just stop a lead in that suit.
Test 3: This hand has 16 HCP (6-losers) and with the ♦K-x could be considered a balanced hand. The recommended bid is 2NT. Despite finding a fit in ♥'s this tells Partner that all high cards will be valuable. Partner can 'Pass', or bid 3♥, 3NT, or 4♥. Remember Partner could have supported Opener with an unbalanced 5 HCP, and now has the possibility to mention a poor 6-card side suit (e.g. 1♥ - 2♥ - 2NT - 3♦). With the sequence 1♥ - 2♥ there is no risk of Opener misinterpreting a very weak distributional 3♦. Remember Partner would have bid game if they were holding anything more than 8+ HCP and 3+ useful cards.
Test 4: This is easy, there is no combination of 'two good cards' with Partner that would offer suggest anything but a 'Pass'.
Test 5: Opener bid with only 11 HCP (13 DH) but 7-losers. Even attributing 2 Aces to Partner (Two Card Rule) there is no possibility of game. So opener might consider to 'Pass'. However the partnership might have only 16-18 HCP, and if so there is a chance that one of the opponent is holding 10-12 HCP and could find a part-score with 2♠ or even a competitive 3♠. So the recommended re-bid of Opener is a non-invitational 3♥. For beginners the sequence 1♥ - 2♥ - 3♥ is invitational. However, we have seen that 2NT (1♥ - 2♥ - 2NT) or a change of suit (1♥ - 2♥ - 3♦) is invitational, so this sequence is not invitational and for experienced players it is a kind of mini-pre-empt (blocking a potential competitive intervention from the opponents).
With the sequence 1♥ - 2♥ - 2NT we must now look at what Partner does after Opener bids 2NT? Opener is telling Partner that they have a fairly balanced hand (15-18 HCP), and that they are interested in all Partners HCP. This is easy. Partner has promised something between 5-10 HCP, and Opener is already expecting (hoping) for a couple of good honour cards. So if Partner replied 2♥ with a minimum (say 5-7 HCP) then they should 'Pass', but if Partner replied with a maximum 9 HCP (even if it's counting Queens and Jacks) then they should bid game.
With ♠J-5 ♥Q-J-8-4 ♦A-7-6-5 ♣10-8-3 bid 4♥
With ♠K-9-8 ♥K-10-4 ♦6-3 ♣Q-9-7-6-5 bid 3NT (maximum points but only 3-card support), Opener can correct to 4♥
With ♠Q-7-6 ♥K-9-8-3 ♦J-7 ♣9-8-7-4 bid 3♥ (with a poor 6 HCP this is a minimum expression of a preference for ♥ with a 4-card ♥, with a 3-card ♥ a 'Pass' would be justified)
With ♠6-4 ♥K-8-3 ♦J-9-7-5 ♣Q-8-6-4 'Pass' with a balanced hand and only 3-card support
With ♠9 ♥Q-8-6 ♦Q-J-9-6-4-3 ♣10-4-2 bid 3♦. This not a forcing bid, remember this follows from a weak 2♥. It is an expression of distribution with poor HCP, a 3-card ♥ and a 6-card ♦. Opener would normally 'Pass' but could prefer a 3♥ with a 5-3 split, or a gamble 3NT, but in any case Partner will 'Pass' on whatever Opener bids.
What to do if Opener bids a second suit (e.g. 1♥ - 2♥ - 3♣)? Just as with the 1♥ - 2♥ - 2NT, this usually promises 15-18 HCP and a useful 4-card minor, and is asking Partner to re-evaluate their hand in both ♥'s and ♣'s. Taking as an example the sequence 1♥ - 2♥ - 3♣:-
With ♠10-7-6 ♥Q-8-6-3 ♦J-9-4-3 ♣A-8 bid 4♥. This hand has a 4-card support with an honour, and the Ace doubleton in Openers second suit.
With ♠Q-5-3 ♥Q-9-8-6 ♦Q-8-6-5 ♣8-3 bid 3♥. This hand has a 4-card support with an honour, and a useful doubleton in Openers second suit (ruffing potential). But the two unprotected side Queens make it a weak hand, thus the bid of 3♥.
With ♠9-7-5-3 ♥Q-10-6-4 ♦K-10-9-4 ♣7 bid 4♥. With 4-card trumps with a honour, a side King and a singleton in Opener's second suit, this 5 HCP becomes 9 DH, and worth a game try. If Partners hand was ♠9-7-5-3 ♥Q-10-6 ♦K-10-9-6-4 ♣7 it would be a sign-off in 3♥ because of the 3-card ♥, but with ♠9-7-5-3 ♥Q-10-6 ♦A-10-9-6-4 ♣7 it would be (again) a 4♥ game bid.
With ♠8-7-5 ♥Q-9-6 ♦K-Q-10-9-7 ♣J-2 bid 3♦. This hand is maximum with 9 DH and a good 5-card ♦. Only 3-card support for ♥ but with a honour, and poor ♣'s. This suggests a game try in NT, but Opener must decide.
Responder makes a game try
The above hands were about Opener receiving support from Partner, and then deciding on the opportunity to make a game try.
However, it is perfectly possible that the suit of Responder or Partner is agreed, and thus it is the Partners decision concerning a game try, e.g. 1♣ - 1♥ - 2♥. Now its Partners suit that is agreed, and it is Partner who must decide. This situation is potentially more complex, the simple raise by Opener suggests a near minimum opening hand 11-14 HCP (13+ DH) but can hide quite a variety of distributions (see below).
Distribution 1: ♠K-5-3 ♥Q-8-6-4 ♦8 ♣A-Q-10-8-6 with 13 DH and only 6-losers, open 1♣ and support Partner in ♥'s.
Distribution 2: ♠8 ♥K-5-3 ♦Q-8-6-4 ♣A-Q-10-8-6 again with 13 DH and only 6-losers, open 1♣ but then Opener has to decide between either 1NT with a un-balanced hand or support Partner with 3-cards.
Distribution 3: ♠K-Q-6 ♥J-10-7-3 ♦K-9-4 ♣K-10-9 is a sterile 4-3-3-3 with 12 HCP. The only option is to open 1♣ and support Partners ♥'s, but perhaps Opener should not have opened.
These three distributions are typical for someone playing 5-card majors and a strong No Trump. The rebid of Partners ♥'s can mean different things, e.g. honest support but bidding with a singleton, or only a 3-card support but still bidding additional value, or a hand that is probably not really worth an opening bid.
Try these tests where Opener started with 1♣, you bid 1♥, and Opener supports you with 2♥, now what do you bid?
Test 1: ♠Q-8-3 ♥A-10-7-6-4 ♦Q-9-7 ♣K-4
Test 2: ♠10-3 ♥A-J-10-8-6 ♦Q-8-6-4 ♣K-2
Test 3: ♠K-2 ♥Q-7-6-3-2 ♦Q-5-3-2 ♣Q-8
Test 4: ♠A-Q-4-3 ♥Q-9-8-7-6-3 ♦10 ♣5-4
Test 5: ♠A-6 ♥K-J-9-7-5 ♦10-4 ♣Q-8-7-6
Answers:
Test 1: Responder has 11 HCP but with a 5-card ♥ (their 1♥ promised a 4-card suit), and a doubleton. The ♣K could be useful with Openers 1♣ bid, but at least one of the Queens will drop, and both could be useless if Opener has 5-4 in ♣'s and ♥'s. Experts suggest a Responder bid of a game invite 2NT but asking for Opener to consider their whole hand, and not one particular suit.
Test 2: Responder has 10 HCP but with a 5-card ♥ (their 1♥ promised a 4-card suit), and a doubleton with a useful ♣K. There is another rule from Forrester called the 'Rule of Nineteen' which added the HCP to the number of cards held in the two longest suits, and if the total comes to 19 or more then a game try is justified, otherwise stop. So the expert advice is bid 3♦.
Test 3: Responder has 10 HCP a 5-card ♥ and a 4-card ♦, and the 'rule of nineteen' holds as well. But the suits are weak and K-J and Q-8 are exposed. Experts suggest a 'Pass'.
Test 4: Responder has 8 HCP but with a 6-card ♥, a 4-card ♠ and a singleton and doubleton. This hand has only 18 points for the 'rule of nineteen' but is worth a bid anyway (so it looks as if the 'rule of nineteen' is not fixed in stone). Change the ♥Q to a ♥A and a 4♥ bid is more than justified, but the experts prefer an invitation bid of 2♠.
Test 5: Responder has 10 HCP but a 5-card ♥, a 4-card ♣ and two doubletons, one with an Ace. Now that ♥ is decided, a bid of 3♣ is a game-try with a 4-card ♣. It just like bidding a new suit and is not a non-forcing reply to Openers 1♣ bid.
Remember the sequence 1♣ - 1♥ - 2♥ - (2NT, 2♠, 3….) are game-try bids and are forcing for one round. In this sense 1♣ - 1♥ - 2♥ - 3♥ is not a game-try invitation.
And what does Opener do now?
But what does Opener do now in front of a sequence 1♣ - 1♥ - 2♥ - (2NT, 2♠, 3….)? Opener is forced to bid. If Responder bids a new suit it promises 10-11 HCP and a 5-4 distribution (note the 5-4 and not a 4-4). If Responder bids 2NT it promises about 11 HCP and a balanced hand (could still have a 5-card ♥ but normally Opener would expect 4-3-3-3 or 4-4-3-2).
If Responder bids 2NT Openers options are 3♥ with minimum and poor HCP and a 4-card ♥, bid 4♥ with a useful 13-14 DH and a 4-card ♥, bid a new 4-card suit below 3♥ or 3NT showing maximum 14 HCP and only 3-card support ♥, or bid 3NT showing a balanced 14 HCP.
On the second round if Responder bids 2♠, 3♣ or 3♦, Openers options are 3♥ with minimum and poor HCP a 4-card ♥ and little help in Responders second suit. Opener can bid a game 4♥ with 13-14 DH and help in Responders second suit (minimum would be a K-x help). Opener should be helpful with a 12-13 HCP with good controls, but cautious even with 13-14 HCP with few controls (e.g. no Aces) and exposed honours and honour sequences.
Special cases, or not so special after all
Let's look at this sequence 1♥ - 1♠ - 2♣ - 2♥. Opener has a 12-19 DH and a 5-4 distribution, and Responder has a 4-card ♠, max. 9 HCP and prefers ♥'s to ♣'s, but is probably only holding a 2-card ♥ (and could easily be holding only a 3-card ♣).
With ♠6 ♥A-J-9-7-6 ♦K-Q-4 ♣A-J-8-6 Opener has shown 16+ DH and a 5-4 distribution, and in front of a weak Partner with only a 2-card ♥, there is little or no possibility of game. The experts suggest a 'Pass'.
With ♠7 ♥K-Q-10-8-4 ♦A-Q-6 ♣K-Q-J-3 Opener has 17 HCP (the singleton in ♠ is worth nothing since Partner bid 1♠). In addition Partner has only a 2-card ♥, so an Opener rebid of 2NT will show 16-17 HCP and an interest in the strength of the Partner (who can Pass in 2NT, or close in 3♥ or 3NT or 4♥).
With ♠Q-5 ♥A-K-J-6-4 ♦9 ♣A-Q-8-3-2 Opener has 16 HCP but a 5-5 distribution, so the expert advice is to bid again 3♣. Partner can 'Pass' or correct to 3♥, or bid game.
Now we get to the really hard part. Both Opener and Partner have bid twice, e.g. 1♣ - 1♥ - 2♥ - 2NT - ?, then what? Franky by now both parties should have a good idea if they should or should not be bidding game. The only question is in what? If Opener has a balanced 14 HCP, they should bid 3NT. With 14-15 HCP but a semi-balanced hand with a weak 4-card support and protected short suits, bid 3NT ('protected' could just mean Q-J through to A-Q). With a minimum 12-13 HCP and a flat distribution 4-3-3-3, even with 4-card support, 'Pass'. With a 12-13 HCP but a singleton in an unbid suit, insist on playing 3♥. With 15-17 DH and good quality support for Partner bid 4♥.
With bidding that goes 1♣ - 1♥ - 2♥ - 2♠ - ?, the situation is very similar to the above, except Partner is asking about strength (honours or ruffing potential) in ♠ (could just as easily be asking for ♣'s or ♦'s). By now the reader should be fairly clear about the options, if not go back and read everything again.
Competitive bidding
Cue-bidding in competitive auctions is a powerful tool, but does it means control through and singleton or void, or with an honour? The difference can make the difference in hand evaluation.
Consider 1♠ - (2♥) - 3♥ - (Pass) - ?, where 3♥ is game forcing with support in ♠'s. What do you bid?
3♠ - no singleton or void, but good hand, open to bidding controls for slam, but would stop at 3NT
3NT - to play
4♣, 4♦, 4♥ - singleton or void
4♠ - no singleton or void, minimum hand.
What would you bid with these hands?
♠A-Q-8-7-4 ♥3 ♦K-J-9 ♣Q-10-9-4 - bidding 4♥ for the singleton/void will still need a lot from Partner, just bid 4♠
♠K-J-6-4-2 ♥6 ♦A-Q-7-6 ♣K-8-7 - same as above, just bid 4♠
♠A-K-8-7-3 ♥7 ♦Q-J-8 ♣A-8-7-4 - it's asking more than a minimum from Partner, some might bid 4♥ just in case, some would just bid 4♠ (a strong Partner might continue)
♠Q-J-10-9-5-3 ♥10 ♦A-8-7 ♣A-K-8 - certainly worth bidding 4♥ for the singleton/void, slam chance, would you push if Partner just bid 4♠?
Slam or no slam
You opened and the bidding went as follows 1♠ - 2♣ - 2♦ - 2♥ - 3♣ - 3♠ - 4♠, what do you think now with your Opening hand?
♠J-7-5-3-2 ♥A ♦K-Q-J-7 ♣J-5-3 - honours not well placed, poor trumps, stop
♠Q-5-4-3-2 ♥6 ♦A-K-Q-5 ♣8-6-4 - honours could be fine, poor trumps, partner would need to invite
♠K-8-7-4-2 ♥K ♦Q-6-5-3 ♣A-9-8 - honours poor in trumps and side suit, stop
♠A-10-9-5-4 ♥J ♦K-Q-9-5 ♣J-5-2 - trumps and honours could be fine, but weak HCP, partner would need to invite.
Now you opened and the bidding went as follows 1♠ - 2♣ - 2♦ - 2♥ - 3♣ - 3♠ - 4♦ - 4♥ - 4♠. You started the cue-bidding (slam seeking controls) with 4♦ and partner replied 4♥. Why close at 4♠?
♠A-J-6-5-4 ♥6 ♦K-Q-J-7 ♣6-5-3 - honours well placed, but stop
♠A-K-10-5-3 ♥5 ♦K-J-10-5 ♣8-7-2 - now has 2 10's, partner would need to invite
♠Q-10-6-4-3 ♥10 ♦A-K-J-7 ♣Q-10-4 - 10's also important, partner would need to invite
♠Q-J-9-4-2 ♥J ♦A-K-10-3 ♣Q-J-10 - good hand, partner would need to invite, but would bid slam
You opened and the bidding went as follows 1♠ - 2♣ - 2♦ - 2♥ - 3♣ - 3♠ - 4♣ - 4♦ - 5♣. Was Partners a real 2♣? What is Partners distribution and point range? Would you have bid 5♣ with these hands? What were your alternatives?
♠K-7-6-5-4 ♥9 ♦K-J-9-6 ♣A-K-5 - poor trumps, clearly Partner has 3-4-3-3 and >16 HCP and 4♦ was a control so all the controls are in place, should have bid 5♠ inviting Partner to Pass or bid 6♠ with good honours
♠K-J-10-4-3 ♥5 ♦Q-J-8-7 ♣A-K-6 - bid 4♥ (control), and not 4♣, showing a lack of control in ♦'s
♠A-Q-10-9-7 ♥3 ♦J-10-3-2 ♣A-K-J - ♦'s are a problem, bid 5♠, and only continue if Partner bids 5♦'s
♠K-Q-10-4-2 ♥8 ♦Q-10-6-3 ♣A-K-10 - solid ♠'s, good 10's, if Partner bids only 5♠'s, Pass otherwise slam
You open and the bidding went as follows 1♠ - 2♣ - 2♦ - 2♥ - 3♣ - 3♠ - 4♣ - 4♦ - ?. What would you bid with these hands?
♠K-Q-J-9-4 ♥6 ♦K-Q-10-5 ♣A-Q-6 - bid 4NT (Blackwood), after 3 key cards, bid 6♣ asking for club honour
♠A-K-10-8-6 ♥5 ♦A-Q-7-6 ♣K-J-7 - bid 4NT (Blackwood), after 5♥ (two key cards, no ♠Q), close with 5♠
♠A-Q—9-7-5 ♥9 ♦A-10-8-6 ♣K-Q-J - bid 4NT (Blackwood), after 3 key cards, bid 6♦ asking Partner for 7♠ with good ♦'s
♠K-J-10-9-4 ♥8 ♦K-Q-J-10 ♣A-K-6 - bid 4NT (Blackwood), with two key cards, no ♠Q, close with 5♠, with 3 key cards bid 6♠.
This final section of shape provided an excellent outline of bidding practices, and is (in my humble opinion) one of the most important topics to be studied and assimilated. The original article is well worth a read since I'm not sure I did it full justice.
References
Evaluation of the Hand – Point Count Adjustment
Two Dimensional Hand Evaluation